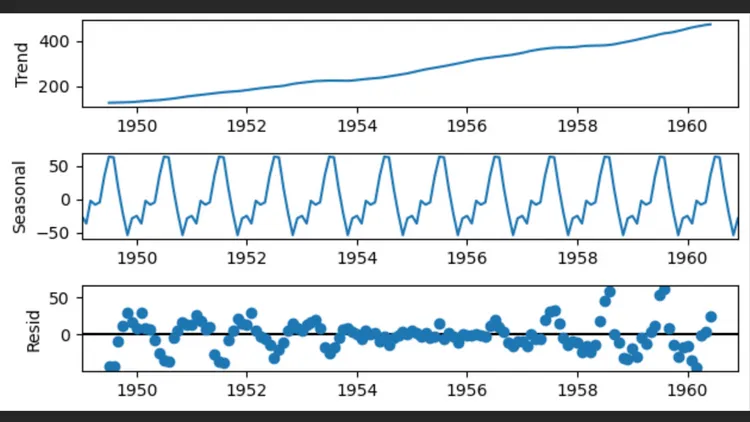
Time Series

What is a Time Series?

A time series is a set of observations recorded at successive time intervals, usually with equal spacing between them. These observations can come from a wide range of contexts, such as economic measurements (for example, a country’s GDP over the years), weather data (such as the daily temperature of a location), sales records (weekly sales of a product), and many others.

The analysis of time series focuses on understanding and modeling how these data evolve over time, in order to make predictions or projections about future values.

The reasons for wanting to make predictions about time series are varied and depend on the field of application. For example, predictions allow for informed decisions about the future, reducing uncertainty. A company can use sales predictions to plan its inventory or an investment in production capacity.

They are also fundamental in strategic planning. This can include everything from the allocation of government budgets to planning the electric power capacity needed to meet future demand.

In engineering and data science, predictions about time series can help optimize processes by foreseeing changes in operating conditions or in the demand for resources.

In finance, the use of these models allows investors and financial analysts to gain a better understanding of the possible direction and volatility of asset prices, which helps in making decisions about when to buy, sell, or hold certain assets in their portfolios. It is also crucial for constructing hedging strategies and for optimizing the risk-return ratio of an investment portfolio.

To make these predictions, various statistical methods and machine learning techniques are used, each with its strengths and limitations depending on the type of time series, the quantity and quality of the data available, and the desired prediction time horizon.

Time Series Modeling Techniques

1. SARIMAX (Seasonal AutoRegressive Integrated Moving Average with eXogenous variables)

This is an extension of the ARIMA model (AutoRegressive Integrated Moving Average), which in turn is widely used for forecasting time series. The SARIMAX model adds support for modeling seasonality and also incorporates exogenous variables, i.e., independent variables that can influence the dependent variable we are trying to predict.

The components of the SARIMAX model can be divided into:

• Autoregression (AR): This component models the dependence between an observation and a number of lagged observations (i.e., in previous periods). It is based on the premise that past values have some effect on current values.
• Integrated Differencing (I): Represents the process of differencing the data to make them stationary. A stationary process is one whose statistical properties, such as mean and variance, are constant over time. Differencing reduces trends and seasonality in the data, allowing the model to focus on the specific fluctuations of the time series.
• Moving Averages (MA): This component models the prediction error as a linear combination of past prediction errors. It helps to smooth fluctuations in the data, capturing the effect of “noise” or random variations.
• S (Seasonal): Represents the seasonal components of the time series, which are patterns that repeat at regular intervals.
• X (eXogenous variables): This component allows incorporating exogenous variables into the model, i.e., additional variables that can influence the time series we are forecasting but are not affected by it.

A SARIMAX model is typically denoted as SARIMAX(p, d, q)x(P, D, Q, s), where:

• p is the number of autoregressive terms (AR component).
• d is the number of differencing needed to make the time series stationary (I component).
• q is the number of moving average terms (MA component).
• P is the number of seasonal autoregressive terms. Similar to p, but applied to the seasonal component of the series.
• D is the degree of seasonal differencing. Similar to d, but to make the series stationary in terms of seasonality.
• Q is the number of seasonal moving average terms. Similar to q, but for past forecast error terms of the seasonal component.
• s is the seasonality period. This parameter indicates the length of the seasonal cycle (for example, 12 for monthly data with annual seasonality).
• Exogenous variables: A set of independent variables that are believed can influence the time series. A matrix or dataframe with the exogenous variables that will be incorporated into the model is provided.

Tuning these parameters is crucial for the model’s performance. Usually, this adjustment is done through grid search procedures or by using information criteria such as the AIC (Akaike Information Criterion) or the BIC (Bayesian Information Criterion) to evaluate different parameter combinations and select the model that best fits the data without overfitting.

The ARIMA model is powerful and versatile, capable of modeling a wide range of time sequences with or without trends and seasonal patterns. However, its efficacy largely depends on the correct identification of parameters and compliance with underlying assumptions.

2. GARCH Models (Generalized Autoregressive Conditional Heteroskedasticity Models)

GARCH models are used to model the volatility of a time series, i.e., how the variability of the series changes over time. They are especially useful when the variance of the time series is not constant (heteroskedasticity). GARCH models can capture patterns such as volatility clustering, where high levels of volatility tend to follow high levels of volatility and vice versa.

3. Machine Learning and Deep Learning

These techniques involve the use of complex computational models that can learn patterns from data.

• Machine Learning: Includes a wide range of techniques, such as decision trees, support vector machines, and ensemble models, that can capture linear and non-linear relationships in the data.

• Deep Learning: It uses neural networks with many layers (deep) to learn complex data representations. LSTM networks (Long Short-Term Memory) are a class of recurrent neural networks (RNNs) designed to address the gradient vanishing problem in learning long-term dependencies. They operate based on the structure of LSTM cells, which allow the network to retain information for long periods and decide what information is relevant to remember or discard through three main components called gates: the forget gate, the input gate, and the output gate.

  1. Forget Gate: Decides what information from the previous state is kept or discarded, using a sigmoid function to assign values between 0 (completely discard) and 1 (completely retain).

  2. Input Gate: Selects what new information will be added to the cell state. It involves two steps: first, a sigmoid function determines which values will be updated; second, a tanh function creates a vector of new candidate values that might be added to the state.

  3. Cell State Update: The cell state is updated by combining the old state, filtered by the forget gate, with the new candidate values, filtered by the input gate.

  4. Output Gate: Determines which part of the cell state will be used for the network’s output. A sigmoid function decides which parts of the state will be activated, and then the cell state is passed through a tanh function and multiplied by the output of the sigmoid to produce the final output of the LSTM cell.

  This gate structure allows LSTMs to manage and maintain long-term memory efficiently, making them particularly useful for applications involving time series, where the ability to remember information from previous inputs is crucial as they can capture long-term dependencies in the data.

4. Factor Models

Factor models explain variations in a time series through a limited number of unobserved (or latent) factors. These factors can represent underlying influences affecting the time series. The model posits that observations are influenced by these factors through specific coefficients, in addition to possibly including error terms to capture other variations not explained by the factors.

Each of these models has its own strengths and applications, and the choice between them depends on the nature of the data and the objectives of the analysis.

Español

¿Qué es una serie temporal?

Una serie temporal es un conjunto de observaciones registradas en intervalos de tiempo sucesivos, usualmente con igual distancia entre ellos. Estas observaciones pueden provenir de muy diversos contextos, como mediciones económicas (por ejemplo, el PIB de un país a lo largo de los años), datos meteorológicos (como la temperatura diaria de una localidad), registros de ventas (ventas semanales de un producto), y muchos otros.

El análisis de series temporales se enfoca en entender y modelar cómo evolucionan estos datos a lo largo del tiempo, para poder realizar predicciones o proyecciones sobre valores futuros.

Las razones para querer hacer predicciones sobre series temporales son muy variadas y dependen del campo de aplicación. Por ejemplo, las predicciones permiten tomar decisiones informadas sobre el futuro, reduciendo la incertidumbre. Una empresa puede usar predicciones de ventas para planificar su inventario o una inversión en capacidad de producción.

También, son fundamentales en la planificación estratégica. Esto puede incluir desde la asignación de presupuestos gubernamentales hasta la planificación de la capacidad de energía eléctrica necesaria para satisfacer la demanda futura.

En la ingeniería y la ciencia de datos, las predicciones sobre series temporales pueden ayudar a optimizar procesos al prever cambios en las condiciones operativas o en la demanda de recursos.

En las finanzas, el uso de estos modelos permite a los inversores y analistas financieros obtener una mejor comprensión de la posible dirección y volatilidad de los precios de los activos, lo que ayuda en la toma de decisiones sobre cuándo comprar, vender, o mantener ciertos activos en sus carteras. También es crucial para la construcción de estrategias de cobertura y para la optimización de la relación riesgo-rendimiento de una cartera de inversiones.

Para hacer estas predicciones, se utilizan diversos métodos estadísticos y de aprendizaje automático, cada uno con sus fortalezas y limitaciones dependiendo del tipo de serie temporal, la cantidad y calidad de los datos disponibles, y el horizonte temporal de la predicción deseada.

Técnicas de modelado de series temporales

1. SARIMAX (Seasonal AutoRegressive Integrated Moving Average with eXogenous variables)

Es una extensión del modelo ARIMA (AutoRegressive Integrated Moving Average), que a su vez es ampliamente utilizado para pronosticar series temporales. El modelo SARIMAX añade soporte para modelar la estacionalidad y también incorpora variables exógenas, es decir, variables independientes que pueden influir en la variable dependiente que estamos tratando de predecir.

Los componentes del modelo SARIMAX se pueden dividir en:

• Autoregresión (AR): Este componente modela la dependencia entre una observación y un número de observaciones retrasadas (es decir, en periodos anteriores). Se basa en la premisa de que los valores pasados tienen algún efecto sobre los valores actuales.
• Diferenciación Integrada (I): Representa el proceso de diferenciación de los datos para hacerlos estacionarios. Un proceso estacionario es aquel cuyas propiedades estadísticas, como la media y la varianza, son constantes a lo largo del tiempo. La diferenciación reduce las tendencias y estacionalidades en los datos, permitiendo que el modelo se enfoque en las fluctuaciones específicas de la serie temporal.
• Medias Móviles (MA): Este componente modela el error de la predicción como una combinación lineal de errores de predicción pasados. Ayuda a suavizar las fluctuaciones en los datos, capturando el efecto de “ruido” o variaciones aleatorias.
• S (Seasonal): Representa los componentes estacionales de la serie temporal, que son patrones que se repiten en intervalos regulares.
• X (eXogenous variables): Este componente permite incorporar variables exógenas al modelo, es decir, variables adicionales que pueden influir en la serie temporal que estamos pronosticando pero que no son afectadas por ella.

Un modelo SARIMAX se denota típicamente como SARIMAX(p, d, q)x(P, D, Q, s), donde:

• p es el número de términos autorregresivos (componente AR).
• d es el número de diferenciaciones necesarias para hacer la serie temporal estacionaria (componente I).
• q es el número de términos de promedio móvil (componente MA).
• P es el número de términos autorregresivos estacionales. Similar a p, pero aplicado a la componente estacional de la serie.
• D es el grado de diferenciación estacional. Similar a d, pero para hacer la serie estacionaria en términos de estacionalidad.
• Q es el número de términos de media móvil estacionales. Similar a q, pero para los términos del error de pronóstico pasado de la componente estacional.
• s es el período de estacionalidad. Este parámetro indica la longitud del ciclo estacional (por ejemplo, 12 para datos mensuales con estacionalidad anual).
• Variables exógenas: Un conjunto de variables independientes que se creen pueden influir en la serie temporal. Se proporciona una matriz o dataframe con las variables exógenas que se incorporarán al modelo.

El ajuste de estos parámetros es crucial para el rendimiento del modelo. Usualmente, este ajuste se realiza mediante procedimientos de búsqueda de cuadrícula o mediante criterios de información como el AIC (Criterio de Información de Akaike) o el BIC (Criterio de Información Bayesiano) para evaluar diferentes combinaciones de parámetros y seleccionar el modelo que mejor se ajuste a los datos sin sobreajustar.

El modelo ARIMA es potente y versátil, capaz de modelar una amplia gama de secuencias temporales con o sin tendencias y patrones estacionales. Sin embargo, su eficacia depende en gran medida de la correcta identificación de los parámetros y del cumplimiento de las suposiciones subyacentes.

2. Modelos GARCH (Modelos Autorregresivos Condicionales Heterocedásticos Generalizados)

Los modelos GARCH son utilizados para modelar la volatilidad de una serie temporal, es decir, cómo la variabilidad de la serie cambia a lo largo del tiempo. Son especialmente útiles cuando la varianza de la serie temporal no es constante (heterocedasticidad). Los modelos GARCH pueden capturar patrones como la agrupación de volatilidad, donde altos niveles de volatilidad tienden a seguirse de altos niveles de volatilidad y viceversa.

3. Machine Learning y Deep Learning

Estas técnicas involucran el uso de modelos computacionales complejos que pueden aprender patrones a partir de los datos.

• Machine Learning: Incluye una amplia gama de técnicas, como los árboles de decisión, las máquinas de soporte vectorial y los modelos de ensamble, que pueden capturar relaciones lineales y no lineales en los datos.

• Deep Learning: Utiliza redes neuronales con muchas capas (profundas) para aprender representaciones de datos complejas. Las redes LSTM (Long Short-Term Memory) son una clase de redes neuronales recurrentes (RNNs) diseñadas para abordar el problema del desvanecimiento del gradiente en el aprendizaje de dependencias a largo plazo. Su funcionamiento se basa en la estructura de celdas LSTM, que permiten que la red retenga información por largos periodos de tiempo y decida qué información es relevante para recordar o descartar a través de tres componentes principales llamados puertas: la puerta de olvido, la puerta de entrada y la puerta de salida.

  1. Puerta de Olvido: Decide qué información del estado anterior se mantiene o se descarta, utilizando una función sigmoide para asignar valores entre 0 (descartar completamente) y 1 (conservar completamente).

  2. Puerta de Entrada: Selecciona qué información nueva se añadirá al estado de la celda. Involucra dos pasos: primero, una función sigmoide determina qué valores se actualizarán; segundo, una función tanh crea un vector de nuevos valores candidatos que podrían añadirse al estado.

  3. Actualización del Estado de la Celda: El estado de la celda se actualiza combinando el estado antiguo, filtrado por la puerta de olvido, con los nuevos valores candidatos, filtrados por la puerta de entrada.

  4. Puerta de Salida: Determina qué parte del estado de la celda se usará para la salida de la red. Una función sigmoide decide qué partes del estado se activarán, y luego el estado de la celda se pasa por una función tanh y se multiplica por la salida de la sigmoide para producir la salida final de la celda LSTM.

  Esta estructura de puertas permite a las LSTM gestionar y mantener una memoria a largo plazo de manera eficiente, lo que las hace particularmente útiles para aplicaciones que involucran series temporales, donde la capacidad de recordar información de entradas antiguas es crucial, ya que pueden capturar dependencias a largo plazo en los datos.

4. Modelos de factores

Los modelos de factores explican las variaciones en una serie temporal mediante un número limitado de factores no observables (o latentes). Estos factores pueden representar influencias subyacentes que afectan a la serie temporal. El modelo establece que las observaciones son influenciadas por estos factores a través de coeficientes específicos, además de posiblemente incluir términos de error para capturar otras variaciones no explicadas por los factores.

Cada uno de estos modelos tiene sus propias fortalezas y aplicaciones, y la elección entre ellos depende de la naturaleza de los datos y los objetivos del análisis.