Time Series Projects

Sep 25, 2023

As part of the application of the theory mentioned in the blog entry:

two projects were developed:

Project 1: AutoARIMA - SARIMA - Prophet - LSTM
Project 2: EDA, K-means, AutoARIMA, Prophet, LSTM

For both projects, the Augmented Dickey-Fuller test, correlograms, and the AutoARIMA model in Python were used.

Augmented Dickey-Fuller Test

The Dickey-Fuller test is a statistical method used to determine if a time series is stationary. A time series is considered stationary if its statistical properties, such as mean and variance, are constant over time.

The values obtained with the implementation of this test in Python are:

ADF Statistic: This is the value used to accept or reject the null hypothesis. A more negative value indicates stronger evidence against the null hypothesis.
p-value: Indicates the probability of observing the data if the null hypothesis were true. A low p-value (for example, < 0.05) suggests that the null hypothesis can be rejected, indicating that the series is stationary.
Critical Values: These are the thresholds needed to reject the null hypothesis with a certain confidence level. If the ADF statistic is less than the critical value for a given significance level (for example, 1%, 5%, 10%), the null hypothesis of a unit root can be rejected, suggesting that the series does not have a unit root and is stationary. Example of interpretation: If the ADF Statistic is less than the critical value at 5%, and the p-value is less than 0.05, there is sufficient evidence to reject the null hypothesis of a unit root. This means that the time series is stationary with 95% confidence.

Correlograms

Correlograms are graphs used in time series analysis to visualize and analyze the autocorrelation (ACF, Autocorrelation Function) and partial autocorrelation (PACF, Partial Autocorrelation Function) in the data. These graphs are fundamental tools for identifying patterns, seasonal trends, and the presence of dependency in the data over time, which can guide the selection of appropriate models for time series analysis.

Autocorrelation Correlogram (ACF)

The ACF measures the linear correlation between the values of the time series and its lags. In simple terms, it tries to quantify how much a observation in the time series resembles its past observations.

What it measures: The ACF measures the linear correlation between the values of the time series at time t and the values at previous times (t-k), for various values of k (where k is the number of lags). It includes the direct and indirect effects of the intermediate values.
Usage: It is useful for identifying the presence of dependency patterns in the data, such as trends or seasonal cycles. An ACF that slowly decreases suggests a Moving Average (MA) model, while a cut after a specific lag suggests an Autoregressive (AR) model.

Partial Autocorrelation Correlogram (PACF)

The PACF measures the correlation between the values of the time series and its lags, eliminating the effects of the intermediate lags. This provides a better view of the direct relationship between an observation and its previous lags.

What it measures: The PACF measures the linear correlation between the values of the time series at time t and the values at previous times (t-k), eliminating the effects of the values at intermediate times (t-1, t-2, …, t-k+1). That is, it measures the correlation between observations separated by k periods, controlling for the values of the intermediate lags.
Usage: The PACF is particularly useful for identifying the order of the autoregressive (AR) components in a model. A significant peak in the PACF at a specific lag k suggests an AR model of order k, as it shows the direct correlation at that lag, excluding the influence of correlations at shorter lags.

Application of Correlograms

ACF and PACF correlograms are primarily applied in the initial stages of time series analysis to help identify the type of statistical model that might be suitable for the data. They are particularly useful in the Box-Jenkins methodology for the identification of ARIMA models, where:

ACF is essential for identifying the need for Moving Average (MA) terms in a model, as patterns such as gradual decrease or sinusoidal behavior indicate the influence of MA components.
PACF helps to identify the number of Autoregressive (AR) terms needed, as an abrupt cut in the PACF suggests the appropriate order for an AR component.

AutoARIMA

In both cases, the AutoARIMA function is used.

In Python, auto_arima is a function provided by the pmdarima library (also known as pyramid-arima) that is used to automatically fit an ARIMA (Autoregressive Integrated Moving Average) model to a time series. auto_arima automatically searches for the most appropriate orders (p, d, q) for the ARIMA model and returns the fitted model.

The auto_arima function uses heuristic methods and search algorithms to find the best ARIMA model based on different criteria, such as minimizing the Akaike Information Criterion (AIC) or the Bayesian Information Criterion (BIC). It takes into account both autoregressive (AR), integrated (I), and moving average (MA) components, as well as seasonal components to handle seasonal patterns in the time series.

The main advantage of auto_arima is that it automates the process of selecting the orders of the ARIMA model, which can save time and effort in finding a suitable model. Additionally, it provides options for considering trends, seasonality, and exogenous components in fitting the model.

Project 1: AutoARIMA - SARIMA - Prophet - LSTM

Visit Notebook (AutoARIMA - SARIMA - Prophet - LSTM)

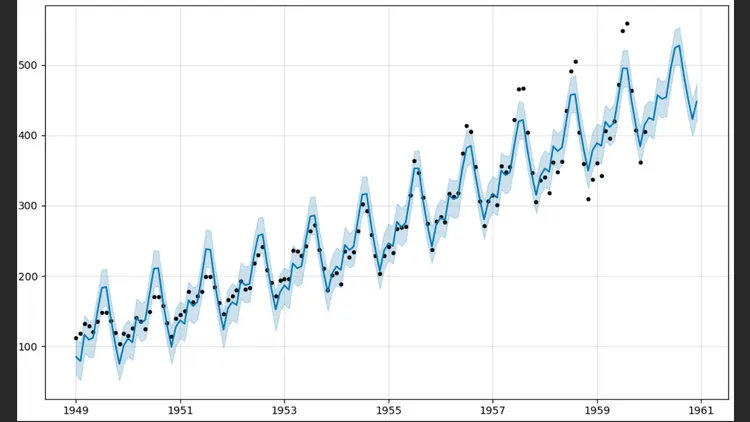
Project 2 is a comprehensive analysis and application of predictive modeling techniques on the “Air Passengers” dataset, which contains data on the number of air passengers per month. Below, each component of the project is detailed, highlighting the objective and methodologies applied in each phase.

1. Moving Averages

The analysis begins with the implementation of moving averages, a basic technique for smoothing the time series and highlighting long-term trends, minimizing the effect of short-term fluctuations or noise.

2. Exponential Moving Average

The exponential moving average (EMA) is applied to give more weight to the most recent data, providing a more sensitive view of recent changes in the number of passengers.

3. Decomposition of Trend and Seasonality

This stage involves decomposing the time series to explicitly identify and separate the components of trend and seasonality, facilitating a clearer understanding of the underlying patterns in the data. seasonal_decompose is used for this purpose.

4. Stationarity Check

A check for the stationarity of the time series is conducted, for which the Dickey-Fuller test was used. This test aims to determine whether a time series is stationary or not. The null hypothesis of this test is that the time series is not stationary.

In this case, the series was not stationary, so several tests were conducted applying shifts of various periods until a stationary series was obtained.

5. Correlogram

The correlogram, or autocorrelation plot, is used to observe and analyze autocorrelation in the data, helping to identify the presence of seasonal or cyclical patterns.

The ACF and PACF are used in the analysis for this phase.

6. Auto ARIMA

The Auto ARIMA model is implemented, which automates the process of selecting ARIMA parameters, seeking the best set of parameters for the model that minimize the information criterion and maximize the prediction accuracy.

For this case, the SARIMAX(2, 1, 2)x(0, 0, [1], 5) model was obtained, which is a seasonal SARIMA model with AR, I, and MA components of orders 2, 1, and 2 respectively, without exogenous variables and with a seasonal pattern of period 5. This model is used to model and predict time series that exhibit both seasonal patterns and trends.

7. SARIMA

The SARIMA model extends ARIMA to include seasonal components, allowing for the modeling of time series with clear seasonal patterns, as is typical in airline passenger data.

The parameters obtained in the previous point are used for the deployment of this model.

8. Prophet

The Prophet algorithm, developed by Facebook, is used for making future predictions. This model is particularly effective for data with strong trends and multiple seasonality.

9. LSTM Network

As the final model, the Long Short-Term Memory (LSTM) network model is used, which is applied to capture long-term dependencies in the data. This type of neural network is suitable for complex time series.

10. RMSE - Root-Mean Square Error

Finally, the performance of the different predictive models is evaluated and compared using the Root-Mean Square Error (RMSE). This metric measures the difference between observed values and the values predicted by the model, allowing for the identification of the most accurate model. In this case, the model obtained with Prophet was the most accurate.

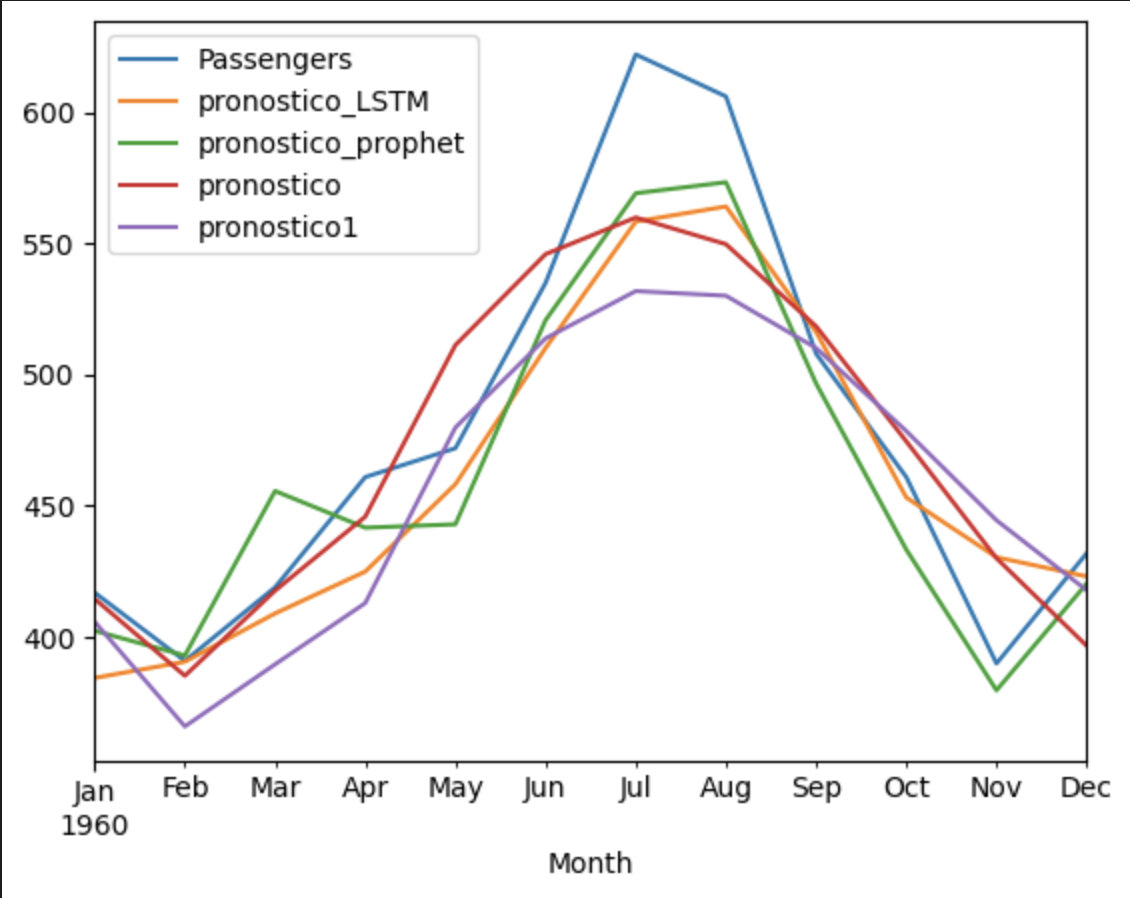
This project demonstrates a rigorous and multifaceted approach to the analysis and predictive modeling of time series, applied in the context of the airline industry. Through a combination of statistical techniques and machine learning, it seeks to deeply understand the dynamics of passenger numbers and predict future trends, providing valuable insights for planning and management in the aviation sector.

Project 2: EDA, K-means, AutoARIMA, Prophet, LSTM

Visit Notebook (EDA, K-means, AutoARIMA, Prophet, LSTM)

The project undertakes a comprehensive analysis and predictive modeling using the “Online Retail Transaction” dataset, which records transactions from an online retail business, including details about products purchased, quantity, price, customer, and country of origin. The breadth and depth of the data present a unique opportunity to extract meaningful insights on buying behaviors and optimize business strategies. Below, each phase of the project is detailed, emphasizing its objective and applied methodologies.

1. Exploratory Data Analysis (EDA)

1.1 Dataset Exploration

Initially, an inspection and preliminary cleaning of the data are performed to understand its structure, detect missing or inconsistent values, and prepare the dataset for further analysis. This step is crucial to ensure the quality and reliability of the insights and predictive models developed subsequently.

1.2 Removing Outliers

Outliers or atypical values that could skew the analysis and modeling are identified and removed. This is done using statistical methods, ensuring that the data accurately reflect the normal trends and patterns of consumer behavior.

1.3 Location Analysis

This analysis seeks to understand the differences in purchasing preferences and customer behaviors according to their geographical location, allowing for regionally adjusted marketing strategies and stock management. It is noted that out of the total 22187 transactions, 19896 were made in the United Kingdom, thus this retail platform has at least 89% of its purchases in that country.

1.4 Product Analysis and Temporal Sales Volume Analysis

The popularity and demand for different products are examined, identifying the best-selling products and their trends over time (by week and by month). This analysis informs inventory management decisions and promotions.

2. Customer Segmentation

2.1 Segmentation by Purchase Frequency

Customers are classified according to the frequency of their purchases to identify regular, occasional, and sporadic buyers, facilitating the personalization of communications and offers. It was referenced that 0-4 is low frequency, 5-9 purchases is medium frequency, and more than 10 purchases is a customer who buys with high frequency.

2.2 Segmentation using K-means

Using the K-means algorithm, customers are grouped into segments based on common characteristics, taking into account: ‘CustomerID’, ‘Frequency’, ‘Quantity’, ‘Total’. This analysis allows for a deeper understanding of the different customer typologies and more specific marketing targeting.

3. Time Series Analysis

3.1 Auto-ARIMA for Product Quantity

It is checked if the series is stationary through the Augmented Dickey-Fuller test. Subsequently, the Auto-ARIMA model is used for calculating the parameters of the SARIMAX model.

3.2 Auto-ARIMA for Dollar Revenue

It is checked if the series is stationary through the Augmented Dickey-Fuller test. Subsequently, the Auto-ARIMA model is used for calculating the parameters of the SARIMAX model.

3.3 SARIMA for Dollar Revenue

When satisfactory parameters are not received through Auto-ARIMA, parameters are obtained manually, using correlograms to get a better idea (autocorrelation and partial autocorrelation). The SARIMA model, which incorporates seasonality into the time series, is applied to predict revenue, capturing periodic patterns in sales.

4. Prophet

4.1 Prophet for Product Quantity

Prophet is employed to predict the quantity of products sold, standing out for its capacity to handle data with trends and seasonal patterns effectively.

4.2 Prophet for Dollar Revenue

Similar to the previous point, but focused on predicting revenue, benefiting from Prophet’s flexibility to incorporate holidays and special events into the model.

5. LSTM

5.1 LSTM for Product Quantity

LSTM networks are applied to model the temporal sequence of product sales, taking advantage of their ability to learn long-term dependencies.

5.2 LSTM for Dollar Revenue

This approach uses LSTM to predict revenue, excelling in handling complex time series and data with long-term dependency patterns.

6. Comparison of RMSE - Root Mean Square Error

6.1 Product Quantity

The performance of the different predictive models for the quantity of products sold is evaluated and compared using RMSE, facilitating the selection of the most accurate model, in this case, were the predictions obtained with the LSTM model.

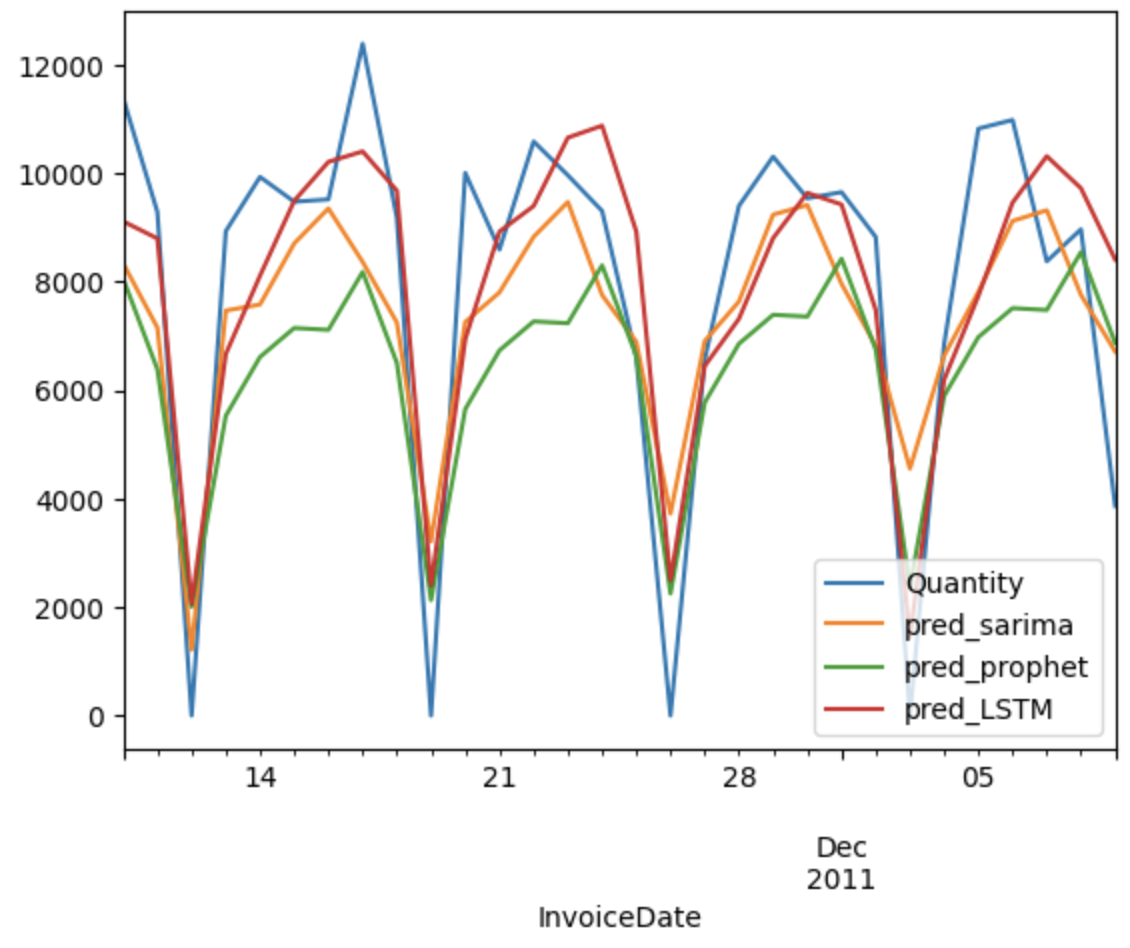
6.2 Dollar Revenue

Similarly, the RMSE for revenue prediction models is compared, determining which offers the most reliable estimates, in this case, were the predictions obtained with Prophet.

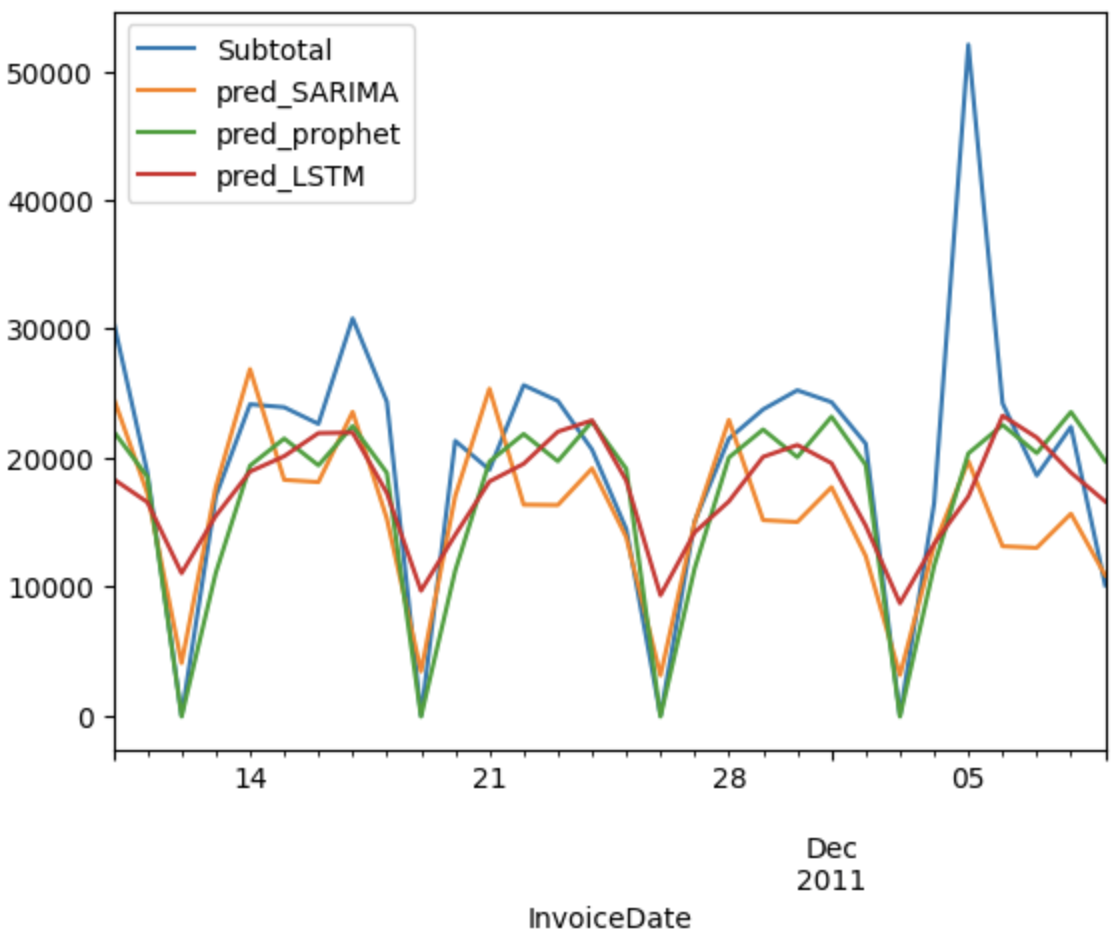
This project demonstrates a holistic approach to understanding and predicting buying behaviors in an e-commerce context, from initial exploratory analysis to the implementation of advanced predictive models, providing a solid foundation for informed decisions in marketing, inventory management, and strategic planning.

Español

Como parte de la aplicación de la teoría mencionada en la entrada del blog:

Time Series

se desarrollan dos proyectos:

Proyecto 1: AutoARIMA - SARIMA - Prophet - LSTM
Proyecto 2: EDA, K-means, AutoARIMA, Prophet, LSTM

para ambos proyectos se hizo uso de la Prueba de Dickey-Fuller aumentada, también de los correlogramas y del modelo AutoARIMA en Python.

Prueba de Dickey-Fuller aumentada

La prueba de Dickey-Fuller es un método estadístico utilizado para determinar si una serie temporal es estacionaria. Una serie temporal se considera estacionaria si sus propiedades estadísticas, como la media y la varianza, son constantes a lo largo del tiempo.

Los valores que se obtienen con la implementación de esta prueba en Python son:

Estadístico ADF (ADF Statistic): Este es el valor que se utiliza para rechazar o no la hipótesis nula. Un valor más negativo indica una mayor evidencia contra la hipótesis nula.
Valor p (p-value): Indica la probabilidad de encontrar los datos observados si la hipótesis nula fuera cierta. Un valor p bajo (por ejemplo, < 0.05) sugiere que se puede rechazar la hipótesis nula, indicando que la serie es estacionaria.
Valores críticos (Critical Values): Son los umbrales necesarios para rechazar la hipótesis nula con un cierto nivel de confianza. Si el estadístico ADF es menor que el valor crítico para un nivel de significancia dado (por ejemplo, 1%, 5%, 10%), se puede rechazar la hipótesis nula de raíz unitaria, sugiriendo que la serie no tiene una raíz unitaria y es estacionaria. Ejemplo de interpretación: Si el ADF Statistic es menor que el valor crítico al 5%, y el p-value es menor que 0.05, hay suficiente evidencia para rechazar la hipótesis nula de que existe una raíz unitaria. Esto significa que la serie temporal es estacionaria con un 95% de confianza.

Correlogramas

Los correlogramas son gráficos utilizados en el análisis de series temporales para visualizar y analizar la autocorrelación (ACF, por sus siglas en inglés Autocorrelation Function) y la autocorrelación parcial (PACF, Partial Autocorrelation Function) en los datos. Estos gráficos son herramientas fundamentales para identificar patrones, tendencias estacionales y la presencia de dependencia en los datos a lo largo del tiempo, lo que puede guiar la selección de modelos adecuados para el análisis de series temporales.

Correlograma de Autocorrelación (ACF)

El ACF mide la correlación lineal entre los valores de la serie temporal y sus retrasos. En términos simples, intenta cuantificar cuánto se parece una observación en la serie temporal a sus observaciones pasadas.

Qué mide: La ACF mide la correlación lineal entre los valores de la serie temporal en un tiempo t y los valores en tiempos anteriores (t-k), para varios valores de k (donde k es el número de retrasos). Incluye los efectos directos e indirectos de los valores intermedios.
Uso: Es útil para identificar la presencia de patrones de dependencia en los datos, como tendencias o ciclos estacionales. Un ACF que disminuye lentamente sugiere un modelo de media móvil (MA), mientras que un corte después de un retraso específico sugiere un modelo autorregresivo (AR).

Correlograma de Autocorrelación Parcial (PACF)

El PACF mide la correlación entre los valores de la serie temporal y sus retrasos, eliminando los efectos de los retrasos intermedios. Esto proporciona una mejor visión de la relación directa entre una observación y sus retrasos anteriores.

Qué mide: La PACF mide la correlación lineal entre los valores de la serie temporal en un tiempo t y los valores en tiempos anteriores (t-k), eliminando los efectos de los valores en tiempos intermedios (t-1, t-2, …, t-k+1). Es decir, mide la correlación entre observaciones separadas por k períodos, controlando por los valores de los retrasos intermedios.
Uso: La PACF es particularmente útil para identificar el orden de los componentes autorregresivos (AR) en un modelo. Un pico significativo en la PACF en un lag específico k sugiere un modelo AR de orden k, dado que muestra la correlación directa a ese lag, excluyendo la influencia de correlaciones en retrasos más cortos.

Aplicación de los Correlogramas

Los correlogramas ACF y PACF se aplican principalmente en las etapas iniciales del análisis de series temporales para ayudar a identificar el tipo de modelo estadístico que podría ser adecuado para los datos. Son particularmente útiles en la metodología Box-Jenkins para la identificación de modelos ARIMA, donde:

ACF es esencial para identificar la necesidad de términos de media móvil (MA) en un modelo, ya que patrones como la disminución gradual o el comportamiento sinusoidal indican la influencia de componentes MA
PACF ayuda a identificar el número de términos autorregresivos (AR) necesarios, ya que un corte abrupto en la PACF sugiere el orden apropiado para un componente AR.

AutoARIMA

En cambos casos se hace uso de la función AutoARIMA

En Python, auto_arima es una función proporcionada por la biblioteca pmdarima (también conocida como pyramid-arima) que se utiliza para ajustar automáticamente un modelo ARIMA (Autoregressive Integrated Moving Average) a una serie de tiempo. auto_arima busca automáticamente los órdenes (p, d, q) más apropiados para el modelo ARIMA y devuelve el modelo ajustado.

La función auto_arima utiliza métodos heurísticos y algoritmos de búsqueda para encontrar el mejor modelo ARIMA según diferentes criterios, como la minimización del criterio de información de Akaike (AIC) o el criterio de información bayesiano (BIC). Toma en cuenta tanto los componentes autoregresivos (AR), integrados (I) y de promedio móvil (MA) como los componentes estacionales para manejar patrones estacionales en la serie de tiempo.

La principal ventaja de auto_arima es que automatiza el proceso de selección de los órdenes del modelo ARIMA, lo que puede ahorrar tiempo y esfuerzo al encontrar un modelo adecuado. Además, proporciona opciones para tener en cuenta tendencias, estacionalidad y componentes exógenos en el ajuste del modelo.

Proyecto 1: AutoARIMA - SARIMA - Prophet - LSTM

Visit Notebook (AutoARIMA - SARIMA - Prophet - LSTM)

El proyecto 2 es un análisis comprensivo y una aplicación de técnicas de modelado predictivo sobre el dataset “Air Passengers”, el cual contiene datos sobre el número de pasajeros aéreos por mes. A continuación, se detalla cada uno de los componentes del proyecto, resaltando el objetivo y las metodologías aplicadas en cada fase.

1. Medias Móviles

El análisis comienza con la implementación de medias móviles, una técnica básica para suavizar la serie temporal y destacar tendencias a largo plazo, minimizando el efecto de fluctuaciones a corto plazo o ruido.

2. Media Móvil Exponencial

Se aplica la media móvil exponencial (EMA) para dar mayor peso a los datos más recientes, proporcionando una visión más sensible a los cambios recientes en el número de pasajeros.

3. Descomposición Tendencia y Estacionalidad

Esta etapa implica descomponer la serie temporal para identificar y separar explícitamente los componentes de tendencia y estacionalidad, facilitando una comprensión más clara de los patrones subyacentes en los datos, se utiliza seasonal_decompose.

4. Verificación de Estacionariedad

Se realiza una verificación de la estacionariedad de la serie temporal, para ellos se hizo uso de la prueba de Dickey-Fuller, la cual busca determinar si una serie de tiempo es estacionaria o no. La hipótesis nula de esta prueba es que la serie de tiempo no es estacionaria.

En este caso la serie no fue estacionaria, por lo que se hicieron varias pruebas aplicando corrimientos de varios periodos hasta que se obtuvo una serie estacionaria.

5. Correlograma

El correlograma, o gráfico de autocorrelación, se utiliza para observar y analizar la autocorrelación en los datos, ayudando a identificar la presencia de patrones estacionales o cíclicos.

Para el desarrollo de esta fase se utiliza en ACF y el PACF dentro del análisis.

6. Auto ARIMA

Se implementa el modelo Auto ARIMA, que automatiza el proceso de selección de los parámetros ARIMA, buscando el mejor conjunto de parámetros para el modelo que minimice el criterio de información y maximice la precisión de la predicción.

Para este caso se obtiene el modelo SARIMAX(2, 1, 2)x(0, 0, [1], 5), el cual es un modelo SARIMA estacional con componentes AR, I y MA de orden 2, 1 y 2 respectivamente, sin variables exógenas y con un patrón estacional de período 5. Este modelo se utiliza para modelar y predecir series de tiempo que exhiben tanto patrones estacionales como tendencias.

7. SARIMA

El modelo SARIMA extiende el ARIMA para incluir componentes estacionales, permitiendo modelar series temporales con patrones estacionales claros, como es típico en los datos de pasajeros aéreos.

Se utilizan los parámetros obtenidos en el punto anterior para el despliegue de este modelo.

8. Prophet

Se utiliza el algoritmo Prophet, desarrollado por Facebook, para realizar predicciones futuras. Este modelo es particularmente efectivo para datos con tendencias fuertes y estacionalidades múltiples.

9. Red LSTM

Como último modelo, se utilizaó el modelo de redes LSTM (Long Short-Term Memory), las cuales se aplican para capturar dependencias a largo plazo en los datos. Este tipo de red neuronal es adecuada para series temporales complejas.

10. RMSE - Root-Mean Square Error

Finalmente, se evalúa y compara el rendimiento de los diferentes modelos predictivos utilizando el error cuadrático medio raíz (RMSE). Este indicador mide la diferencia entre los valores observados y los valores predichos por el modelo, permitiendo identificar el modelo más preciso. En este caso fue el modelo obtenido con Prophet.

Este proyecto demuestra un enfoque riguroso y multifacético para el análisis y modelado predictivo de series temporales, aplicado al contexto de la industria aérea. A través de una combinación de técnicas estadísticas y de machine learning, se busca comprender profundamente la dinámica del número de pasajeros y predecir tendencias futuras, proporcionando insights valiosos para la planificación y gestión en el sector aéreo.

Proyecto 2: EDA, K-means, AutoARIMA, Prophet, LSTM

Visit Notebook (EDA, K-means, AutoARIMA, Prophet, LSTM)

El proyecto aborda un análisis exhaustivo y modelado predictivo utilizando el “Online Retail Transaction” dataset, que registra transacciones de un comercio minorista en línea, incluyendo detalles sobre productos comprados, cantidad, precio, cliente y país de origen. La amplitud y profundidad de los datos presentan una oportunidad única para extraer insights significativos sobre comportamientos de compra y optimizar estrategias comerciales. A continuación, se detalla cada fase del proyecto, enfatizando su objetivo y metodologías aplicadas.

1. Análisis Exploratorio de Datos (EDA)

1.1 Exploración del Dataset

Inicialmente, se realiza una inspección y limpieza preliminar de los datos para entender su estructura, detectar valores faltantes o inconsistentes, y preparar el dataset para análisis posteriores. Este paso es crucial para asegurar la calidad y fiabilidad de los insights y modelos predictivos desarrollados posteriormente.

1.2 Remover Outliers

Se identifican y eliminan los outliers o valores atípicos que podrían sesgar el análisis y la modelación. Esto se hace mediante métodos estadísticos, asegurando que los datos reflejen con precisión las tendencias y patrones normales de comportamiento del consumidor.

1.3 Análisis de Ubicación

Este análisis busca comprender las diferencias en las preferencias de compra y comportamientos de los clientes según su ubicación geográfica, permitiendo estrategias de marketing y stock ajustadas regionalmente. Vemos que del total de transacciones 22187, 19896 fueron realizadas en United Kingdom, por lo tanto esta plataforma de venta al menudeo tiene al menos el 89% de sus compras en ese país

1.4 Análisis de Productos y análisis temporal del volumen de ventas

Se examina la popularidad y la demanda de distintos productos, identificando aquellos más vendidos y sus tendencias a lo largo del tiempo (por semana y por mes). Este análisis informa decisiones de gestión de inventario y promociones.

2. Segmentación de Clientes

2.1 Segmentación por Frecuencia de Compra

Se clasifican los clientes según la frecuencia de sus compras para identificar a los compradores habituales, ocasionales y esporádicos, facilitando la personalización de comunicaciones y ofertas. Se tomó como referencia que de 0-4 es baja frecuencia, de 5-9 compras es media frecuencia y más de 10 compras es un cliente que compra con alta frecuencia

2.2 Segmentación usando K-means

Utilizando el algoritmo de K-means, los clientes se agrupan en segmentos basados en características comunes, tomando en cuenta: ‘CustomerID’, ‘Frequency’, ‘Quantity’, ‘Total’. Este análisis permite una comprensión más profunda de las diferentes tipologías de cliente y una orientación de marketing más específica.

3. Análisis de Serie Temporal

3.1 Auto-ARIMA para Cantidad de Productos

Se comprueba si la serie es estacionaria a través de la prueba de Dickey-Fuller aumentada. Posteriormente se utiliza el modelo Auto-ARIMA para el cálculo de los parámetros del modelo SARIMAX.

3.2 Auto-ARIMA para Ingresos en Dólares

Se comprueba si la serie es estacionaria a través de la prueba de Dickey-Fuller aumentada. Posteriormente se utiliza el modelo Auto-ARIMA para el cálculo de los parámetros del modelo SARIMAX.

3.3 SARIMA para Ingresos en Dólares

Al no recibir parámetros satisfactorios mediante Auto-ARIMA se obtienen los parámetros de forma manual, se utilizan los correlogramas para tener una mejor idea (autocorrelación y autocorrelación parcial). Se aplica el modelo SARIMA, que incorpora la estacionalidad en la serie temporal, se utiliza para predecir los ingresos, capturando patrones periódicos en las ventas.

4. Prophet

4.1 Prophet para Cantidad de Productos

Prophet se emplea para predecir la cantidad de productos vendidos, destacando por su capacidad de manejar datos con tendencias y patrones estacionales de manera efectiva.

4.2 Prophet para Ingresos en Dólares

Similar al punto anterior, pero enfocado en predecir ingresos, beneficiándose de la flexibilidad de Prophet para incorporar días festivos y eventos especiales en el modelo.

5. LSTM

5.1 LSTM para Cantidad de Productos

Las redes LSTM se aplican para modelar la secuencia temporal de ventas de productos, aprovechando su habilidad para aprender dependencias a largo plazo.

5.2 LSTM para Ingresos en Dólares

Este enfoque utiliza LSTM para predecir los ingresos, destacando en el manejo de series temporales complejas y datos con patrones de dependencia a largo plazo.

6. Comparación de RMSE - Root Mean Square Error

6.1 Cantidad de Productos

Se evalúa y compara el rendimiento de los diferentes modelos predictivos para la cantidad de productos vendidos usando el RMSE, facilitando la selección del modelo más preciso, en este caso fueron las predicciones obtenidas con el modelo LSTM

6.2 Ingresos en Dólares

Similarmente, se compara el RMSE para los modelos de predicción de ingresos, determinando cuál ofrece las estimaciones más fiables, en este caso fueron las predicciones obtenidas con Prophet.

Este proyecto demuestra un enfoque holístico para entender y predecir comportamientos de compra en un contexto de comercio electrónico, desde el análisis exploratorio inicial hasta la implementación de modelos predictivos avanzados, proporcionando una base sólida para decisiones informadas en marketing, gestión de inventario y planificación estratégica.